11. 排序与查找

11.1. 算法的概念

算法（ Algorithm） 是将一组输入转化成一组输出的一系列计算步骤， 其中每个步骤必须能在有限时间内完成。 比如 递归 习题 1 中的 Euclid 算法，输入是两个正整数， 输出是它们的最大公约数， 计算步骤是取模、 比较等操作， 这个算法一定能在有限的步骤和时间内完成（ 想一想为什么？）。 再比如将一组数从小到大排序， 输入是一组原始数据， 输出是排序之后的数据， 计算步骤包括比较、 移动数据等操作。

算法是用来解决一类计算问题的，注意是一类问题，而不是一个特定的问题。例如，一个排序算法应该能对任意一组数据进行排序，而不是仅对 int a[] = { 1, 3, 4, 2, 6, 5 }; 这样一组数据排序，如果只需要对这一组数据排序可以写这样一个函数来做：

void sort(void)
{
    a[0] = 1;
    a[1] = 2;
    a[2] = 3;
    a[3] = 4;
    a[4] = 5;
    a[5] = 6;
}

这显然不叫算法，因为不具有通用性。由于算法是用来解决一类问题的，它必须能够正确地解决这一类问题中的任何一个实例，这个算法才是正确的。对于排序算法，任意输入一组数据，它必须都能输出正确的排序结果，这个排序算法才是正确的。不正确的算法有两种可能，一是对于该问题的某些输入，该算法会无限计算下去，不会终止，二是对于该问题的某些输入，该算法终止时输出的是错误的结果。有时候不正确的算法也是有用的，如果对于某个问题寻求正确的算法很困难，而某个不正确的算法可以在有限时间内终止，并且能把误差控制在一定范围内，那么这样的算法也是有实际意义的。例如有时候寻找最优解的开销很大，往往会选择能给出次优解的算法。

本章介绍几种典型的排序和查找算法，并围绕这几种算法做时间复杂度分析。学完本章之后如果想进一步学习，可以参考一些全面系统地介绍算法的书，例如 [TAOCP] 和 [算法导论] 。

11.2. 插入排序

插入排序算法类似于玩扑克时抓牌的过程，玩家每拿到一张牌都要插入到手中已有的牌里，使之从小到大排好序。例如（该图出自 [算法导论] ）：

扑克牌的插入排序

也许你没有意识到， 但其实你的思考过程是这样的： 现在抓到一张 7， 把它和手里的牌从右到左依次比较， 7 比 10 小， 应该再往左插， 7 比 5 大， 好， 就插这里。 为什么比较了 10 和 5 就可以确定 7 的位置？ 为什么不用再比较左边的 4 和 2 呢？ 因为这里有一个重要的前提： 手里的牌已经是排好序的。 现在我插了 7 之后， 手里的牌仍然是排好序的， 下次再抓到的牌还可以用这个方法插入。

编程对一个数组进行插入排序也是同样道理，但和插入扑克牌有一点不同，不可能在两个相邻的存储单元之间再插入一个单元，因此要将插入点之后的数据依次往后移动一个单元。排序算法如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
/**
 * 插入排序
 */
#include "readarray.h" // 引入 readarray 函数, 用于从 10int.array 中获取数据
#include <stdio.h>

// typedef struct {
//     int length;
//     int *body;
// } array_t;

/**
 *  使用插入法将数组排序为从小到大的序列
 *  将序列划分为 "已排序", "未排序" 两个部分
 *
 *  1. 从未排序部分选中一个基准位值
 *  2. 在已排序部分从后向前依次选择, 将元素向后挪, 当找到一个比此位小的值,
 *     则 将 key 插入到此值之后
 *  3. 将已排序部分向后伸展一位
 *
 *  :param array: 要处理的数组, 此结构体指针在整个程序中不会指向其他位置
 *  :param counter: 计数器, 一次调用增加一
 */
void insertion_sort(const array_t *array, int *counter) {
  int key;          // 选择基准位值
  int sorted_i = 0; // 已排序部分的索引
  int j;            // 当前操作位置

  while (sorted_i < array->length && *counter < 1000) { // 防止失败而陷入死循环
    printarray(array, *counter);
    (*(counter))++;
    // 选出未排序部分中的一个元素
    key = array->body[sorted_i];
    // 在已排序部分中进行比较
    for (j = sorted_i; j > 0; --j) {
      if (array->body[j] < key) {
        array->body[j + 1] = key;
        ++sorted_i; // 成功排序一位
        break;
      } else {
        array->body[j] = array->body[j - 1];
      }
    }
    // 如果排到了头部, 则说明 key 在已排序部分最小, 将他插到第一位
    if (j == 0) {
      array->body[j] = key;
      ++sorted_i; // 成功排序一位
    }
  }
}

int main(void) {
  array_t array;
  int counter = 0;
  readarray("10int.array", &array);
  insertion_sort(&array, &counter);
  printarray(&array, -1);
  return 0;
}

为了更清楚地观察排序过程，我们在每次循环开头插了打印语句，在排序结束后也插了打印语句。程序运行结果是:

 0:  96,  93,   0,   0,   2,  73,  21,  73,  30,  46,
 1:  96,  93,   0,   0,   2,  73,  21,  73,  30,  46,
 2:  93,  96,   0,   0,   2,  73,  21,  73,  30,  46,
 3:   0,  93,  96,   0,   2,  73,  21,  73,  30,  46,
 4:   0,   0,  93,  96,   2,  73,  21,  73,  30,  46,
 5:   0,   0,   2,  93,  96,  73,  21,  73,  30,  46,
 6:   0,   0,   2,  73,  93,  96,  21,  73,  30,  46,
 7:   0,   0,   2,  21,  73,  93,  96,  73,  30,  46,
 8:   0,   0,   2,  21,  73,  73,  93,  96,  30,  46,
 9:   0,   0,   2,  21,  30,  73,  73,  93,  96,  46,
-1:   0,   0,   2,  21,  30,  46,  73,  73,  93,  96,

这个来自 Wikipedia 的 GIF 图也许能给你带来直观的印象:

https://upload.wikimedia.org/wikipedia/commons/0/0f/Insertion-sort-example-300px.gif

如何严格证明这个算法是正确的？ 换句话说， 只要反复执行该算法的外层 for 循环体， 执行 length-1 次， 就一定能把数组 array 排好序， 而不管数组 array 的原始数据是什么， 如何证明这一点呢？ 我们可以借助 循环不变性 的概念和数学归纳法来理解循环结构的算法， 假如某个判断条件满足以下三条准则， 它就称为 循环不变性：

  1. 第一次执行循环体之前该判断条件为真。
  2. 如果 “第 N-1 次循环之后（ 或者说第 N 次循环之前） 该判断条件为真” 这个前提可以成立， 那么就有办法证明第 N 次循环之后该判断条件仍为真。
  3. 如果在所有循环结束后该判断条件为真，那么就有办法证明该算法正确地解决了问题。

只要我们找到这个 循环不变性 ，就可以证明一个循环结构的算法是正确的。上述插入排序算法的 循环不变性 是这样的判断条件：第 j 次循环之前，子序列 array[0 .. j-1] 是排好序的。在上面的打印结果中， 我在最前面标注了子序列是前多少位 。下面我们验证一下 循环不变性 的三条准则：

  1. 第一次执行循环之前， j=1 ，子序列 a[0..j-1] 只有一个元素 a[0] ，只有一个元素的序列显然是排好序的。
  2. 第 j 次循环之前，如果 “子序列 a[0..j-1] 是排好序的” 这个前提成立，现在要把 key=a[j] 插进去，按照该算法的步骤，把 a[j-1] 、 a[j-2] 、 a[j-3] 等等比 key大的元素都依次往后移一个，直到找到合适的位置给 key 插入，就能证明循环结束时子序列 a[0..j] 是排好序的。就像插扑克牌一样，“手中已有的牌是排好序的”这个前提很重要，如果没有这个前提，就不能证明再插一张牌之后也是排好序的。
  3. 当循环结束时， j=length ，如果“子序列 a[0..j-1] 是排好序的”这个前提成立，那就是说 a[0..length-1] 是排好序的，也就是说整个数组 array 的 length 个元素都排好序了。

可见，有了这三条，就可以用数学归纳法证明这个循环是正确的。这和 递归 证明递归程序正确性的思想是一致的，这里的第一条就相当于递归的 Base Case，第二条就相当于递归的递推关系。这再次说明了递归和循环是等价的。

11.3. 算法的时间复杂度分析

解决同一个问题可以有很多种算法，比较评价算法的好坏，一个重要的标准就是算法的时间复杂度。现在研究一下插入排序算法的执行时间，按照习惯，输入长度 length 以下用 n 表示。设循环中各条语句的执行时间分别是 \(c_1, c_2, c_3\) 这样三个常数 [1] ：

void insertion_sort(int* array, size_t length)   // 执行时间
{
    int key;
    int i;

    for (int j = 1; j < length; j++) {
        key = array[j];                     // c_1
        for (i = j - 1; i >= 0; i--) {
            if (array[i] > key) {           // c_2, 表示整个 if 结构
                array[i + 1] = array[i];
            } else {
                break;
            }
        }
        array[i + 1] = key;                 // c_3
    }

显然外层 for 循环的执行次数是 \(n-1\) 次，假设内层的 for 循环执行 \(m\) 次，则总的执行时间粗略估计是 \((n-1) (c_1 + c_3 + m c_2)\) 。当然， for 循环 后面括号中的赋值和条件判断的执行也需要时间，而我没有设一个常数来表示，这不影响我们的粗略估计。

这里有一个问题， \(m\) 不是个常数，也不取决于输入长度 \(n\) ，而是取决于具体的输入数据。在最好情况下，数组 a 的原始数据已经排好序了，内层 for 循环一次也不执行，总的执行时间是 \((n-1)*(c_1 + c_3)\) ，可以表示成 \(an+b\) 的形式，是 \(n\) 的线性函数（Linear Function） 。那么在最坏情况（Worst Case） 下又如何呢？所谓最坏情况是指数组 a 的原始数据正好是从大到小排好序的，这意味着需要从头到尾重新排序，把上式中的 \(m\) 替换掉算一下执行时间就是:

\[m = \sum_{i=1}^{n-1} i = \frac{n}{2}\]

则总时间为

\[T = (n-1)(c_1 + c_3 + \frac{c_2 n}{2}) = \frac{c_2}{2} n^2 + \frac{2c_1 + 2c_3 - c_2}{2} - (c_1 + c_3)\]

数组a的原始数据属于最好和最坏情况的都比较少见，如果原始数据是随机的，可称为平均情况（Average Case） 。如果原始数据是随机的，那么每次循环将已排序的子序列 a[1..j-1] 与新插入的元素 key 相比较，子序列中都存在一些元素比 key 大而另一些比 key 小， 导致 \(m\) 能有所积累。最后的结论应该是：在最坏情况和平均情况下，总的执行时间都可以表示成 \(a n^2 + b n + c\) 的形式，是 \(n\) 的二次函数（Quadratic Function） 。

在分析算法的时间复杂度时，我们更关心最坏情况而不是最好情况，理由如下：

  1. 最坏情况给出了算法执行时间的上界，我们可以确信，无论给什么输入，算法的执行时间都不会超过这个上界，这样为比较和分析提供了便利。
  2. 对于某些算法，最坏情况是最常发生的情况，例如在数据库中查找某个信息的算法，最坏情况就是数据库中根本不存在该信息，都找遍了也没有，而某些应用场合经常要查找一个信息在数据库中存在不存在。
  3. 虽然最坏情况是一种悲观估计，但是对于很多问题，平均情况和最坏情况的时间复杂度差不多，比如插入排序这个例子，平均情况和最坏情况的时间复杂度都是输入长度 \(n\) 的二次函数。

比较两个多项式 : \(a_1 n+ b_1\) 和 \(a_2 n_2+b_2 n+c_2\) 的值（ \(n\) 取正整数）可以得出结论： \(n\) 的最高次指数是最主要的决定因素，常数项、低次幂项和系数都是次要的。比如 \(100n+1\) 和 \(n2+1\) ，虽然后者的系数小，当 \(n\) 较小时前者的值较大，但是当 \(n>100\) 时，后者的值就远远大于前者了。如果同一个问题可以用两种算法解决，其中一种算法的时间复杂度为线性函数，另一种算法的时间复杂度为二次函数，当问题的输入长度 \(n\) 足够大时，前者明显优于后者。因此我们可以用一种更粗略的方式表示算法的时间复杂度，把系数和低次幂项都省去，线性函数记作 \(\Theta(n)\) ，二次函数记作 \(\Theta(n^2)\) 。

\(\Theta(g(n))\) 表示和 \(g(n)\) 同一量级的一类函数，例如所有的二次函数 \(f(n)\) 都和 \(g(n)=n^2\) 属于同一量级，都可以用 \(\Theta(n^2)\) 来表示，甚至有些不是二次函数的也和 \(n^2\) 属于同一量级，例如 \(2 n^2+ 3 \operatorname{lg} n\) 。“同一量级”这个概念可以用下图来说明（该图出自 [算法导论] ）：

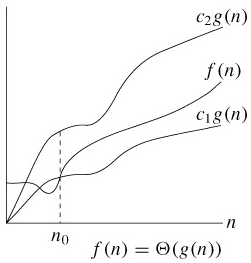
Theta-notation

如果可以找到两个正的常数 \(c_1\) 和 \(c_2\) ，使得 \(n\) 足够大的时候（也就是 \(n \ge n_0\) 的时候） \(f(n)\) 总是夹在 \(c_1 g(n)\) 和 \(c_2g(n)\) 之间，就说 \(f(n)\) 是同一量级的， \(f(n)\) 就可以用 \(\Theta(g(n))\) 来表示。

以二次函数为例，比如 \(\frac{1}{2} n^2-3n\) ，要证明它是属于 \(\Theta(n^2)\) 这个集合的，我们必须确定 \(c_1, c_2, n_0\) ，这些常数不随 \(n\) 改变，并且当 \(n \ge n_0\) 以后， \(c_1 n^2 \le \frac{1}{2} n^2 - 3n \le c_2 n^2\) 总是成立的。为此我们从不等式的每一边都除以n2，得到 \(c_1 \le \frac{1}{2} - \frac{3}{n} \le c_2\) 。见下图：

1/2-3/n

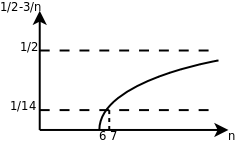
这样就很容易看出来，无论 \(n\) 取多少，该函数一定小于 \(\frac{1}{2}\) ，因此 \(c_2 = \frac{1}{2}\) ，当 \(n=6\) 时函数值为 0 ， \(n>6\) 时该函数都大于 0 ，可以取 \(n_0=7\) ， \(c_1=\frac{1}{14}\) ，这样当 \(n \ge n_0\) 时都有 \(\frac{1}{2} - \frac{3}{n} \ge c_1\) 。通过这个证明过程可以得出结论，当 \(n\) 都夹在 \(c_1 n^2\) 和 \(c_2 n^2\) 之间，相对于 \(n^2\) 项来说 \(bn+c\) 的影响可以忽略， \(a\) 可以通过选取合适的 \(c_1, c_2\) 来补偿。

几种常见的时间复杂度函数按数量级从小到大的顺序依次是 \(\Theta(\lg n), \Theta(\sqrt{n}), \Theta(n), \Theta(n \lg n), \Theta(n^2), \Theta(n^3), \Theta(2^n), \Theta(n!)\) 。其中， \(\lg n\) 通常表示以 10 为底 \(n\) 的对数，但是对于 \(\Theta\) -notation 来说， \(\Theta(\lg n)\) 和 \(\Theta(\log_2 n)\) 并无区别（想一想这是为什么），在算法分析中 \(\lg n\) 通常表示以 2 为底 \(n\) 的对数。可是什么算法的时间复杂度里会出现 \(\lg n\)lg` 呢？下一节 归并排序 的时间复杂度里面就有 \(\lg\) ，请读者留心 \(\lg\) 运算是从哪出来的。

除了 \(\Theta\) -notation 之外，表示算法的时间复杂度常用的还有一种 Big-O notation 。我们知道插入排序在最坏情况和平均情况下时间复杂度是 \(\Theta(n^2)\) ，在最好情况下是 \(\Theta(n)\) ，数量级比 \(\Theta(n^2)\) 要小，那么总结起来在各种情况下插入排序的时间复杂度是 \(O(n^2)\) 。 \(\Theta\) 的含义和“等于”类似，而 \(O\) 的含义和“小于等于”类似。

[1]受内存管理机制的影响，指令的执行时间不一定是常数，但执行时间的上界（Upper Bound） 肯定是常数，我们这里假设语句的执行时间是常数只是一个粗略估计。

11.4. 归并排序

插入排序算法采取增量式（Incremental） 的策略解决问题，每次添一个元素到已排序的子序列中，逐渐将整个数组排序完毕，它的时间复杂度是 \(O(n^2)\) 。下面介绍另一种典型的排序算法－－归并排序，它采取分而治之（Divide-and-Conquer） 的策略，时间复杂度是 \(\Theta(n \lg n)\) 。归并排序的步骤如下：

  1. Divide: 把长度为 \(n\) 的输入序列分成两个长度为 \(\frac{n}{2}\) 的子序列。
  2. Conquer: 对这两个子序列分别采用归并排序。
  3. Combine: 将两个排序好的子序列合并成一个最终的排序序列。

在描述归并排序的步骤时又调用了归并排序本身，可见这是一个递归的过程。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// TODO:
const int gLEN = 8;
int gCOUNT = 0;

void mergeSort(int* array, int length);
extern int* array;
/**
 * 打印目标数组的情况
 */
void printArray()
{
    printf("%2d: ", gCOUNT); // %I64d 是 size_t 类型的格式符
    for (size_t i = 0; i < gLEN; i++) {
        printf("%3d, ", *(array + i));
    }
    printf("\n");
}

int main(void)
{
    srand(time(NULL));
    static int array[gLEN];
    for (int i = 0; i < gLEN; i++) {
        array[i] = rand() % 100;
    }
    mergeSort(array, gLEN);
    return 0;
}

/**
 * 归并排序
 */
void mergeSort(int* array, int length)
{
    gCOUNT++;
    printArray();

    int mid = length >> 1; // 将 length 除以二
    int *left, *right;
    left = array;
    right = array + mid;
    // 拆分数组
    if (mid <= 1) {
        mergeSort(left, mid);
        mergeSort(right, length - mid);
    } else {
        for (int i = 0; i < mid; i++) {
            if (left[i] <= right[i]) {
                array[2 * i] = left[i];
                array[2 * i + 1] = right[i];
            } else {
                array[2 * i] = right[i];
                array[2 * i + 1] = left[i];
            }
        }
    }
}
https://upload.wikimedia.org/wikipedia/commons/c/cc/Merge-sort-example-300px.gif